思路

把圆角矩形分成 9 份，分别是 4 个角（p0p1p5p4、p2p3p7p6、p8p9p13p12、p10p11p15p14），4 个边缘（p1p2p6p5、p4p5p9p8、p6p7p11p10、p9p10p14p13）和 1 个中心（p5p6p10p11）。角的部分画弧，边缘和中心画矩形。

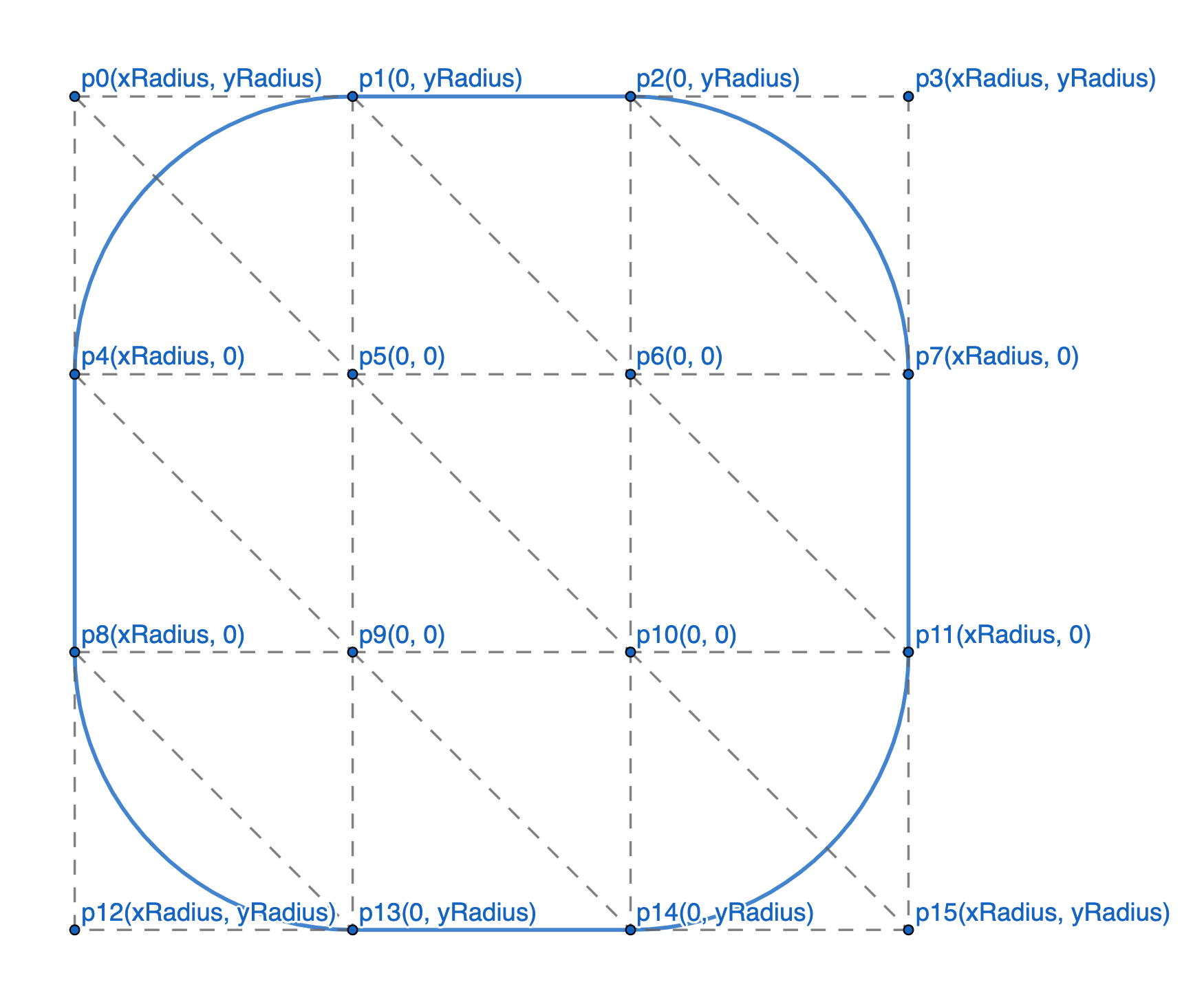
顶点的定义除了常规的屏幕坐标，再提供一个小矩形的坐标，小矩形坐标的作用是计算点到图形轮廓的距离。

传进去的小矩形坐标经过标准化之后，不管是椭圆弧还是圆弧，都转化为半径为 1 的圆弧，根据公式 d = $\sqrt{x^2+y^2}$ - 1 可以计算距离。

中心矩形的小矩形坐标 x, y 都是 0；边缘四个矩形的小矩形坐标要么 x 是 0，要么 y 是 0，所以它计算的是点到边缘直线的距离。角上四个矩形的小矩形坐标计算的是点到圆弧的距离。

点到轮廓的距离为正，在图形外，alpha 为 0；为负在图形内，为 0 在图形上，alpha 为 1。

实现抗锯齿时，整个图形的坐标数据扩大 0.5px，用于 coverage 的计算。coverage 的范围是图形轮廓内外各 0.5px，加起来是 1px，也就是点到轮廓的距离[-0.5px, 0.5px]，对应的 alpha 值为[0, 1]。

如果是圆弧的时候，上面的实现没问题，抗锯齿也完成的很好；但是如果是椭圆弧的时候，上面的实现就会出现下面的现象。比如按照比例缩小椭圆 80%，短半径从 5 到 4，长半径从 10 到 8，就是那个实线-内椭圆，和实线-外椭圆相比，它们之间的距离不是均匀的，而我们想要的是距离均匀的椭圆，也就是虚线的椭圆。

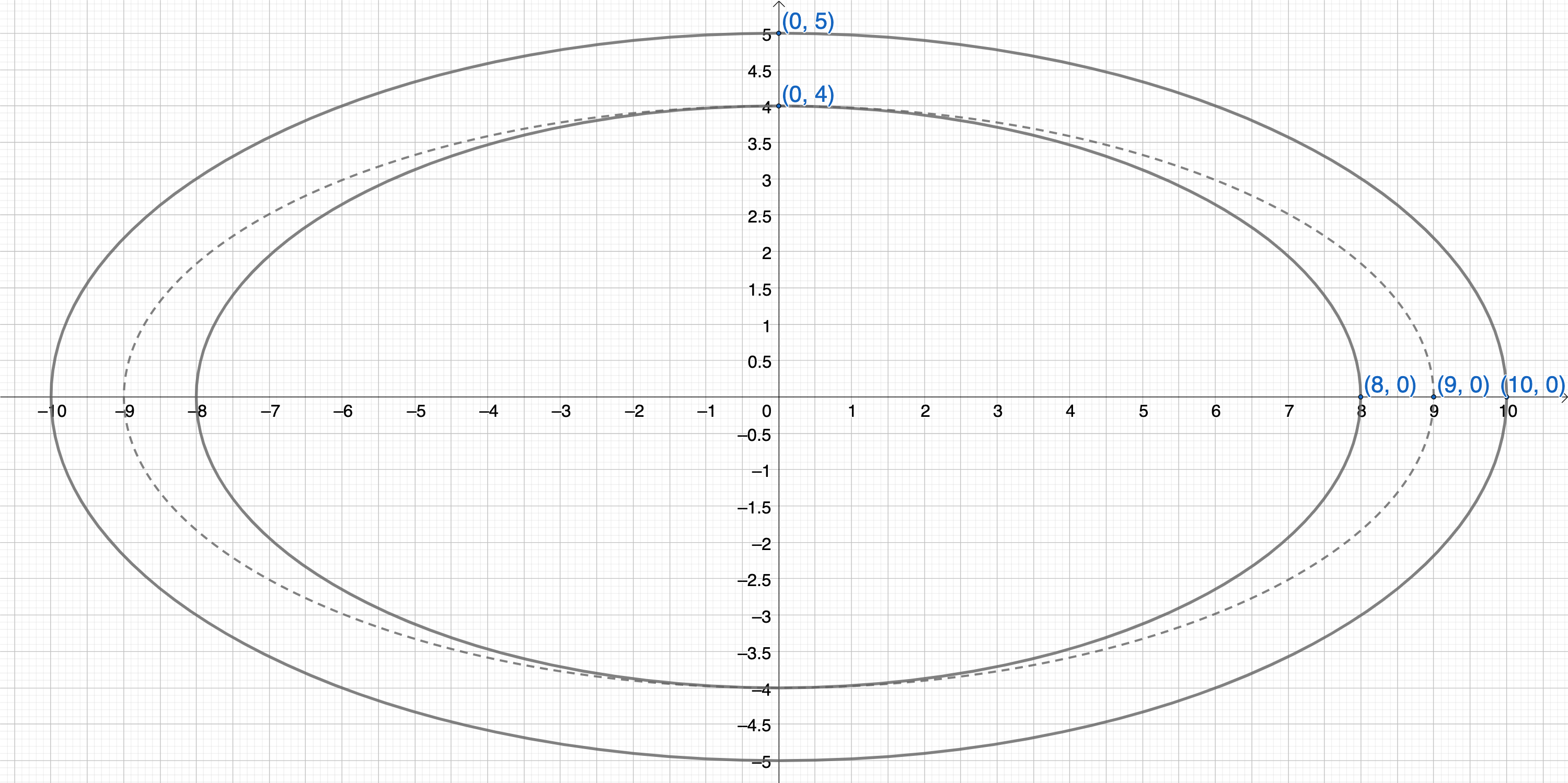
所以上面的公式不适合用在椭圆上。

通过 skia 分享的 ppt，我们知道有一个公式可以计算点到椭圆的近似距离。

这个公式一般用来检测椭圆，也就是通过一些离散的点来拟合椭圆。

$d \approx \frac{f(x, y)}{|\nabla f(x, y)|}$ —> $d \approx \frac{\frac{x^2}{a^2}+\frac{y^2}{b^2}-1}{\sqrt{(\frac{2x}{a^2})^2+(\frac{2y}{b^2})^2}}$

可以从下面的链接找到这个公式的证明： Fitting conic sections to “very scattered” data: An iterative refinement of the Bookstein algorithm。

vertex shader

1
2
3
4
5
6

attribute vec2 inPosition; // 屏幕坐标
attribute vec2 inEllipseOffset; // 小矩形坐标
attribute vec2 inEllipseRadii; // 椭圆 1/a, 1/b

varying vec2 vEllipseOffsets_Stage0 = inEllipseOffset;
varying vec2 vEllipseRadii_Stage0 = inEllipseRadii;

fragment shader

1
2
3
4
5
6
7

vec2 offset = vEllipseOffsets_Stage0*vEllipseRadii_Stage0;
float test = dot(offset, offset) - 1.0;
vec2 grad = 2.0*offset*vEllipseRadii_Stage0;
float grad_dot = dot(grad, grad);
grad_dot = max(grad_dot, 1.1755e-38);
float invlen = inversesqrt(grad_dot);
float edgeAlpha = clamp(0.5-test*invlen, 0.0, 1.0);

顶点的 index 数据，18 个三角形

1
2
3
4
5
6
7
8
9
10
11
12
13
14

// corners  
0, 1, 5, 0, 5, 4,
2, 3, 7, 2, 7, 6,
8, 9, 13, 8, 13, 12,
10, 11, 15, 10, 15, 14,

// edges  
1, 2, 6, 1, 6, 5,
4, 5, 9, 4, 9, 8,
6, 7, 11, 6, 11, 10,
9, 10, 14, 9, 14, 13,

// center  
5, 6, 10, 5, 10, 9,

上面说的是画一个填充的圆角矩形，还可以画一个 stroke 的圆角矩形，有兴趣可以看下 skia 的GrOvalFactory.cpp

链接

skia
DrawingAntialiasedEllipse
Sampson, P.D.: Fitting conic sections to “very scattered” data: An iterative refinement of the Bookstein algorithm. Comput. Graphics Image Process. 18, 97-108
Evaluating Harker and O’Leary’s Distance Approximation for Ellipse Fitting